 |
 |
 |
 |
 |
Der Satz des Pythagoras
„Der weise Pythagoras,Der die Schrift der Sterne las:Der war so weise sonder Streit,Dass niemand seit Adams ZeitNoch so weisen Sinn getragen; ...”(Wolfram von Eschenbach, Parzival,
übertragen von Karl Simrock)
Der Satz und sein Beweis
Er ist der berühmteste Satz der Mathematik. Jeder hat ihn gehört. Benannt ist er nach einem altgriechischen Mathematiker, Philosophen, Zahlenmystiker, Begründer einer Geheimgesellschaft, der um 550 v. Chr. lebte und ein Schüler des Thales von Milet war, welchem bekanntlich ein ebenso grundlegender Satz zugeschrieben wird. Der Sachverhalt selber war lange vor Pythagoras bekannt, und das nicht nur im griechischen Kulturkreis. Die Ägypter kannten ihn, die Babylonier, die indischen Mathematiker, die Chinesen. Er ist ja auch so naheliegend, zumindest wenn man sich mit geometrischen Fragen befasst.
Ausgangspunkt soll die Aufgabe sein, ein Quadrat zu verdoppeln. Gemeint ist, ein neues Quadrat mit dem doppelten Flächeninhalt herzustellen. Die Animation verdeutlicht die Lösung.
Die ist so einfach und einleuchtend, dass die Frage nach der Verdopplung eines Würfels sich fast von selber stellt. Aber daran sind Jahrhunderte intensiven Bemühens gescheitert. Wie man heute weiß, musste der Versuch scheitern, weil man mit Zirkel und Lineal nur solche Probleme lösen kann, die sich durch lineare oder quadratische Gleichungen ausdrücken lassen. Die Verdoppelung des Würfels verlangt die Lösung der kubischen Gleichung x3 = 2·a3

Zurück zum Satz des Pythagoras. Das in der Mitte der Animation gelb hervorgehobene Dreieck ist rechtwinklig, und es ist symmetrisch. Die beiden Kathetenquadrate sind gleich groß, sie ergeben zusammen die Fläche des Hypotenusenquadrates – zu den Benennungen vergleiche die nebenstehende Skizze. Wie aber, wenn die Katheten und mithin auch die Kathetenquadrate unterschiedlich sind?
In diesem Fall bilden wir aus den beiden – blauen – Kathetenquadraten und vier Exmplaren des – gelben – rechtwinkligen Dreiecks ein neues größeres Quadrat. Hokuspokus lassen sich die die Dreiecke so verschieben, dass die Kathetenquadrate verschwinden und – pink – das Hypotenusenquadrat erscheint. Und weil sich an der Gesamtfläche währenddem nichts geändert hat, zeigt dies die Gleichheit des Hypotenusenquadrates mit den beiden Kathetenquadraten zusammengenommen.
Es gilt also
Zum Satz des Pythagoras gibt es inzwischen eine unüberschaubare Menge von Beweisen, teils geometrischer, teils algebraischer Natur. Einen Eindruck von dieser Fülle bietet z. B. cut-the-knot. (22.1.2020)
Die Bedeutung des Satzes
Was eigentlich ist das Besondere dieses Satzes? Sein Inhalt ist einfach zu verstehen, sein Beweis ist leicht nachvollziehbar. Und doch ist seine Aussage nicht so banal, dass sie ohne Weiteres einleuchtet. Dass die Kathetenquadrate zusammen die Fläche des Hypotenusenquadrates ergeben, „sieht” man nicht. Man muss es erst bewiesen bekommen, damit man es glaubt. Eine einfache Aussage, die trotzdem des Beweises bedarf – das gibt dem Satz des Pythagoras seine besondere Stellung im Lehrplan.
Dazu kommt die immense praktische Bedeutung dieses Satzes. Schon in der Antike war er zentrales Hilfsmittel. Wenn die griechische Mathematik, die im Wesentlichen Geometrie war, eine Fläche zu bestimmen hatte, suchte sie ein entsprechendes Quadrat. Hatte sie zu mehreren Teilflächen die Quadrate gefunden, musste sie diese zu einem Gesamtquadrat zusammensetzen. Das leistete der Satz des Pythagoras.
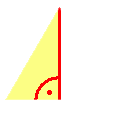
Heute dient er uns meistens dazu, Längen zu berechnen. Um die Fläche eines gleichseitigen Dreiecks mit der Seitenlänge s zu bestimmen, benötigt man seine Höhe h. Das gelbe Teildreieck ist rechtwinklig, die Hypotenuse ist s, die Katheten sind h und s/2. Der Satz des Pythagoras liefert die Gleichung
| s2 | = | h2 | + | ( | s | )2 | . |
| 2 |
Aufgelöst nach h ergibt sich
| h2 | = | s2 | − | s2 | , |
| 4 | |||||
| h | = | s | √3 | . | |
| 2 |
Danach kann man mit „Fläche = Grundlinie mal Höhe durch 2” die Dreiecksfläche berechnen.
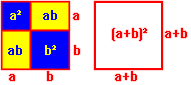
Die Animation zum Satz des Pythagoras ist noch in anderer Hinsicht hilfreich. Sie kann als eine Illustration zur ersten binomischen Formel
Pythagoräische Zahlen
Bemerkenswerterweise hat ein rechtwinkliges Dreieck mit den Katheten 3cm und 4cm nach dem Satz des Pythagoras die Hypotenuse 5cm, denn es ist 32 + 42 = 9 + 16 = 25 = 52. Es gibt also rechtwinklige Dreiecke mit ganzzahligen Seitenlängen. Wenn man ein wenig sucht, findet man noch weitere, z. B. 5cm, 12cm und 13cm. Allein unter den Zahlen bis 100 findet man schon 51 solcher „pythagoräischer Zahlentripel”.
Wie kann man diese pythagoräischen Zahlentripel finden? Durch Probieren, natürlich. Aber es gibt eine elegantere Möglichkeit. Zu zwei beliebigen natürlichen Zahlen p und q, die beide größer als null sind und von denen außerdem p die größere ist, bildet man
| a2 + b2 | = (p2 − q2)2 + (2pq)2 |
| = p4 − 2p2q2 + q4 + 4p2q2 | |
| = p4 + 2p2q2 + q4 | |
| = (p2 + q2)2 | |
| = c2. |
Aber erhält man damit auch alle pythagoräischen Zahlentripel? Zumindest die primitiven, die teilerfremden Zahlentripel lassen sich so gewinnen. (6, 8, 10) ist nicht primitiv, man erzeugt es aus (3, 4, 5) durch Multiplikation mit 2. In einem primitiven Zahlentripel müssen schon je zwei Zahlen teilerfremd sein, denn sonst hätte auch die dritte denselben Teiler, insbesondere können a und b nicht beide gerade sein.
a und b können aber auch nicht beide ungerade sein, denn dann müsste c2, mithin auch c selber gerade sein, c2 also 4 enthalten, während a2 + b2 zwar auch gerade wäre, die 4 aber nicht enthielte, wie folgende Rechnung zeigt (dabei sei a = 2i+1 und b = 2j+1):
| a2 + b2 | = (2i+1)2 + (2j+1)2 |
| = 4i2 + 4i + 1 + 4j2+4j + 1 | |
| = 4(i2 + i + j2 +j) + 2. |
Nehmen wir also an, a ist die ungerade, b die gerade von den beiden. Auch c ist dann ungerade. Wir setzen a = 2i+1, b = 2j, c = 2k+1 und erhalten:
| a2 + 4j2 | = c2, |
| 4j2 | = c2 − a2 |
| = (c+a) · (c−a) | |
| = (2k+2i+2) · (2k−2i) | |
| = 4 · (k+i+1) · (k−i). |
Nun sind (k+i+1) und (k−i) teilerfremd, denn hätten sie einen gemeinsamen Teiler, dann wäre dieser auch Teiler ihrer Summe 2k+1=c und ihrer Differenz 2i+1=a, im Gegensatz zu unserer obigen Bemerkung. Das bedeutet, dass auch (c+a)/2 und (c−a)/2 teilerfremd sind. Da ihr Produkt das Quadrat j2 ergibt, muss jeder dieser Ausdrücke für sich eine Quadratzahl sein. Wir setzen p für die Wurzel aus (c+a)/2 und q für die Wurzel aus (c−a)/2. Damit ergibt sich
| p2 | − | q2 | = | c | + | a | − | c | − | a | = | a, |
| 2 | 2 | |||||||||||
| 2 | p | q | = | √ | c2 | − | a2 | = | b, | |||
| p2 | + | q2 | = | c | + | a | + | c | − | a | = | c. |
| 2 | 2 |
Das primitive Tripel (a, b, c) lässt sich also wie gewünscht konstruieren. Und hier ist eine Tabelle der ersten so gewonnenen pythagoräischen Zahlentripel:
| p | q | a | b | c | |
|---|---|---|---|---|---|
| 2 | 1 | 3 | 4 | 5 | |
| 3 | 1 | 8 | 6 | 10 | |
| 3 | 2 | 5 | 12 | 13 | |
| 4 | 1 | 15 | 8 | 17 | |
| 4 | 2 | 12 | 16 | 20 | |
| 4 | 3 | 7 | 24 | 25 | |
| 5 | 1 | 24 | 10 | 26 | |
| 5 | 2 | 21 | 20 | 29 | |
| 5 | 3 | 16 | 30 | 34 | |
| 5 | 4 | 9 | 40 | 41 | |
| 6 | 1 | 35 | 12 | 37 | |
| 6 | 2 | 32 | 24 | 40 | |
| 6 | 3 | 27 | 36 | 45 | |
| 6 | 4 | 20 | 48 | 52 | |
| 6 | 5 | 11 | 60 | 61 | |
| 7 | 1 | 48 | 14 | 50 | |
| 7 | 2 | 45 | 28 | 53 | |
| 7 | 3 | 40 | 42 | 58 | |
| 7 | 4 | 33 | 56 | 65 | |
| 7 | 5 | 24 | 70 | 74 | |
| 7 | 6 | 13 | 84 | 85 | |
| 8 | 1 | 63 | 16 | 65 | |
| 8 | 2 | 60 | 32 | 68 | |
| 8 | 3 | 55 | 48 | 73 | |
| 8 | 4 | 48 | 64 | 80 | |
| 8 | 5 | 39 | 80 | 89 | |
| 8 | 6 | 28 | 96 | 100 | |
| 8 | 7 | 15 | 112 | 113 |
Man sieht aber, dass z. B. die nicht-primitiven Tripel (9, 12, 15), (15, 20, 25), (18, 24, 30) und (21, 28, 35), die sich alle aus (3, 4, 5) erzeugen lassen, in dieser Tabelle nicht vorkommen, andere wie (12, 16, 20) und (24, 32, 40) dagegen schon.
Die Fermatsche Vermutung
Wenn es so viele Zahlen a, b, c gibt, die die Bedingung a2 + b2 = c2 erfüllen, wie sieht es dann mit den dritten Potenzen aus? Gibt es auch Zahlen, die der Bedingung a3 + b3 = c3 genügen? Es gibt sie nicht. Der Beweis dazu erfordert allerdings tiefere Kenntnis der komplexen Zahlen, ich muss ihn hier schuldig bleiben.
Und für noch höhere Potenzen? Dazu gibt es eine nette Randbemerkung von Pierre de Fermat (1601(?) – 1665) zu Diophants im dritten Jahrhundert verfassten Werk „Arithmetica”:
„Es ist nicht möglich, einen Kubus in zwei Kuben oder ein Biquadrat in zwei Biquadrate [4. Potenzen, Anmerkung Melching] und allgemein eine Potenz, höher als die zweite, in zwei Potenzen mit demselben Exponenten zu zerlegen. Ich habe hierfür einen wahrhaft wunderbaren Beweis, doch ist der Rand hier zu schmal, um ihn zu fassen.”
Diesen „wahrhaft wunderbaren Beweis”
haben seitdem Generationen von Mathematikern vergebens gesucht. Als in den achtziger Jahren des 20. Jahrhunderts der Amerikaner Andrew Wiles schließlich den Beweis erbringen konnte, war der alles andere als wunderbar. Schwerstes mathematisches Geschütz und ein Umfang von beinahe hundert Seiten waren erforderlich. Der wunderbare Beweis kann also weiter gesucht werden. Oder hat Fermat sich am Ende geirrt und sein vermeintlicher Beweis war gar keiner?