 |
 |
 |
 |
 |
Die schönste Gleichung
Die Gleichung
 gilt vielen als die schönste mathematische Gleichung überhaupt. Sie verbindet in konzentrierter Form die fünf wichtigsten Zahlen miteinander, die 0, die 1, die Kreiszahl π, das geheimnisvolle e und die
imaginäre Einheit i.
Wie kommt es, dass diese auf so frappierend bündige Weise zusammen hängen?
gilt vielen als die schönste mathematische Gleichung überhaupt. Sie verbindet in konzentrierter Form die fünf wichtigsten Zahlen miteinander, die 0, die 1, die Kreiszahl π, das geheimnisvolle e und die
imaginäre Einheit i.
Wie kommt es, dass diese auf so frappierend bündige Weise zusammen hängen?
Die Abkürzung 5! (gelesen „5 Fakultät”) bedeutet 1·2·3·4·5 = 120. Mithilfe dieser Abkürzung bilden wir
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | |
| 1! | 2! | 3! | 4! | 5! | 6! | 7! |
| = | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 |
| 1 | 2 | 6 | 24 | 120 | 720 | 5040 |
= 2,718254 .
Das Ergebnis liegt ziemlich nahe bei der Zahl e, die auf 6 Dezimalen gerundet den Wert 2,718282 besitzt. Die Abweichung wäre noch geringer, wenn man weitere Summationsglieder nach demselben Schema hinzunähme. Ja, wenn ich nur weit genug gehe, kann ich diese Abweichung beliebig klein machen. Man sagt,e ist der Grenzwert dieser Summe, die Summe strebt gegen e. Wir wandeln die Summe ein wenig ab und bilden:
| 1 | + | 21 | + | 22 | + | 23 | + | 24 | + | 25 | + | 26 | + | 27 | |
| 1! | 2! | 3! | 4! | 5! | 6! | 7! |
| = | 1 | + | 2 | + | 4 | + | 8 | + | 16 | + | 32 | + | 64 | + | 128 |
| 1 | 2 | 6 | 24 | 120 | 720 | 5040 |
= 7,380953 .
Durch diese Summe erhalten wir – je weiter ausgeführt, umso besser – das Ergebnis e2 = 7,389056. Das trifft nun nicht nur auf den Exponenten 2 zu, sondern sinngemäß auch auf jeden anderen. Allgemein gilt:
| 1 | + | x1 | + | x2 | + | x3 | + | x4 | + | x5 | + | x6 | + | x7 | … | |
| 1! | 2! | 3! | 4! | 5! | 6! | 7! |
Man nennt dies die Reihenentwicklung der Exponentialfunktion. (Für den Leistungskurs Mathematik: es handelt sich hier um die sogenannte Taylor-Reihe, für deren Erzeugung es ein überschaubares Verfahren gibt, das allerdings etwas Integralrechnung erfordert.) Auch für andere Funktionen kennt man eine solche Reihenentwicklung. So hat die Sinusfunktion die Entwicklung
| x1 | − | x3 | + | x5 | − | x7 | + | x9 | − | x11 | + | x13 | − | x15 | … | |
| 1! | 3! | 5! | 7! | 9! | 11! | 13! | 15! |
| 1 | − | x2 | + | x4 | − | x6 | + | x8 | − | x10 | + | x12 | − | x14 | … | |
| 2! | 4! | 6! | 8! | 10! | 12! | 14! |
Das x muss dazu, wie in weiten Bereichen der Mathematik üblich, im Bogenmaß angegeben werde, also nicht 360o, sondern 2π, nicht 180o, sondern π, nicht 90o, sondern π/2 usw.) In den obigen Formeln deuten sich bereits rätselhafte Zusammenhänge an. Denen wollen wir nachgehen. Dazu erinnern wir uns an die besondere Eigenschaft der imaginären Einheit i :
Wir bilden jetzt eiπ. Dabei ersparen wir uns die letzte mathematische Genauigkeit, wohl wissend, dass der Umgang mit unendlichen Summen und ihren Grenzwerten nicht unproblematisch ist. Eine Vorstellung von den Zusammenhängen gewinnt man auf diese Weise gleichwohl. Die Farben sollen uns dabei helfen, in den langen Gleichungszeilen den Überblick zu behalten und zu erkennen, wie die Dinge sich entwickeln.
| eiπ | = | 1 | + | (iπ)1 | + | (iπ)2 | + | (iπ)3 | + | (iπ)4 | + | (iπ)5 | + | (iπ)6 | + | (iπ)7 | … | |
| 1! | 2! | 3! | 4! | 5! | 6! | 7! | ||||||||||||
| = | 1 | +i | π 1 | − | π 2 | −i | π 3 | + | π 4 | +i | π 5 | − | π 6 | −i | π 7 | … | ||
| 1! | 2! | 3! | 4! | 5! | 6! | 7! | ||||||||||||
| = | 1 | − | π 2 | + | π 4 | − | π 6 | … | ||||||||||
| 2! | 4! | 6! | ||||||||||||||||
| + | i ( | π 1 | − | π 3 | + | π 5 | − | π 7 | … | ) | ||||||||
| 1! | 3! | 5! | 7! | |||||||||||||||
| = | cos | (π) | +i | sin | (π) | |||||||||||||
| = | −1 | +i | 0 | |||||||||||||||
| = | −1 | . | ||||||||||||||||
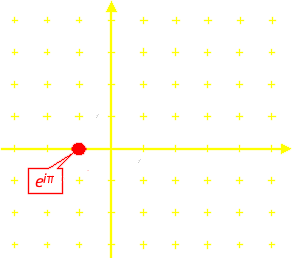
Aus dieser Gleichheit folgt der eingangs angegebene Satz unmittelbar. Anschaulich bedeutet es, dass eiπ in der Zahlenebene an dieser Stelle liegt:
Und noch eine abschließende Bemerkung für den Leistungskurs Mathematik: Wenn man die Reihenentwicklung von ex,
| ex | = | 1 | + | x | + | x2 | + | x3 | + | x4 | + | x5 | + | x6 | + | x7 | … | , | |
| 2! | 3! | 4! | 5! | 6! | 7! |
| 0 | + | 1 | + | 2· | x1 | + | 3· | x2 | + | 4· | x3 | + | 5· | x4 | + | 6· | x5 | + | 7· | x6 | … | |
| 2! | 3! | 4! | 5! | 6! | 7! | |||||||||||||||||
| = | 1 | + | x | + | x2 | + | x3 | + | x4 | + | x5 | + | x6 | … | ||||||||
| 2! | 3! | 4! | 5! | 6! | ||||||||||||||||||
| = | ex | . | ||||||||||||||||||||
Diese besondere Eigenschaft der e-Funktion, dass sie und ihre Ableitungsfunktion miteinander identisch sind, ist einer der Gründe, warum die Mathematiker diese Funktion so lieben. Nicht nur das Differenzieren, sondern auch das ansonsten häufig vertrackte Integrieren ist hier das reine Vergnügen.