Taschenrechner

Ein Taschencomputer für den Mathematikunterricht
Erwartungen und Befürchtungen

(abgedruckt im Jahresbericht 2002 des Gymnasiums Melle)

„Dass die niedrigste aller Geistestätigkeiten die arithmetische sei, wird dadurch belegt, dass es die einzige ist, die auch von Maschinen ausgeführt werden kann.”(Schopenhauer)

Nun ist es also beschlossen. Ein neues Gerät soll den Mathematikunterricht bereichern. Lange wurde die Angelegenheit diskutiert, kontrovers, wie es bei einer so weitreichenden Entscheidung unausweichlich ist, mit der Suche nach Alternativen, mit unerfüllbaren Wünschen, mit Hoffnungen und Zweifeln. Am Ende eine Entscheidung, mehrheitlich, entsprechend unserer Kultur der Entscheidungsfindung, und der Wunsch, fortbestehende Bedenken mögen sich bei der praktischen Arbeit relativieren.

Unsere Schüler sollen am Ende alles beherrschen, das kleine Einmaleins und die Integralrechnung, den Dreisatz und die Interpretation von statistischen Daten, den Satz von Pythagoras und die Geometrie mehrdimensionaler Gebilde. Und sie sollen auch verstehen, dass man die Mathematik braucht, um sich in der Welt von heute zurechtzufinden. Das ist viel verlangt und erfordert immer wieder, sich der Hilfsmittel zu versichern, die den Zugang zur Mathematik erleichtern und die Vertrautheit mit Mathematik fördern.

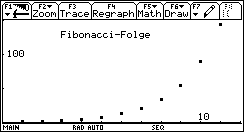
Ein Ausnahmegenie wie Carl-Friedrich Gauß konnte souverän auf allen Instrumenten spielen. Er hatte eine unmittelbare Anschauung der Zahlen, ihrer Struktur und ihrer Zusammenhänge (sozusagen das kleine Einmaleins). Er drang tief in mathematisches Neuland vor und erforschte dort Kontinente, die vor ihm noch niemand betreten hatte. Er verstand etwas von praktischen Problemen und nutzte sein immenses Wissen, z. B. im Vorantreiben der Telegraphie, der Landvermessung, der Analyse von Messwerten. Und doch bediente er sich, um neue Vermutungen aufzuspüren oder zu überprüfen, der Dienste eines Rechenkünstlers, wie sie damals, und auch heute noch verschiedentlich, im Zirkus auftraten und die Zuschauer mit wahnsinnigen Rechenfertigkeiten verblüfften.

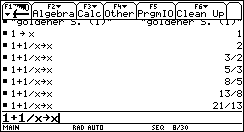
Der Übergang vom mittelalterlichen zum neuzeitlichen, vom geozentrischen zum heliozentrischen Weltbild ist exemplarisch verknüpft mit den Namen Kopernikus, Galilei und Kepler. Als Johannes Kepler das vorliegende Datenmaterial des Tycho Brahe nutzen wollte, um seinen theoretischen Ansatz zur Planetenbewegung wissenschaftlich zu untermauern, benötigte er für die aufwändigen Rechnungen eine Logarithmentafel. Die war zwar schon erfunden, aber noch nicht zu haben, der Erfinder Jobst Bürgi kam damit nicht recht zu Potte, so hat Kepler sich eine solche flugs selber erstellt. Sie leistete das Erwartete, und das sogar, obwohl in den Tausenden von Rechnungen sich irgendwo im letzten Drittel ein Rechenfehler eingeschlichen hatte.

Rechenhilfen gelten im allgemeinen Bewusstsein längst als legitim. An der Supermarktkasse haben wir es alle eilig und sind froh, dass dort wenigstens das Addieren schnell geht. Im Restaurant sehen wir das schon etwas anders. Eine an der Kellnerkasse erstellte Rechnung mit Hotelkopf und Mehrwertsteueranteil ist o.k, eine Bedienung, die am Tisch mit einem Taschenrechner hantiert, gilt als leicht beschränkt. Noch vor zwei Jahrzehnten gehörte neben dem kleinen auch das große Einmaleins zur Allgemeinbildung, auf Kopfrechnen und auf die Vermittlung von Rechenvorteilen wurde großer Wert gelegt. Heute benutzen wir dazu Taschenrechner.

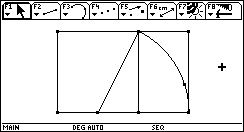
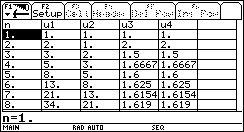
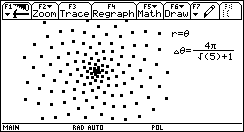
Taschenrechner rechnen mit Zahlen. Sie sind die moderne Form der vordem so hilfreichen Rechenschieber und Logarithmentafeln. Inzwischen können solche Geräte aber weitaus mehr. Sie haben genug Platz, um alle Rechnungen einer Arbeitssitzung aufzubewahren und auf Abruf zurückzuholen. Sie können auf Knopfdruck umfangreiche Tabellen erzeugen, erweitern, verändern. Sie können Tabellen, aber auch beliebige andere mathematische Funktionen graphisch darstellen - solche Visualisierungen tragen wesentlich zum Verständnis bei, sind aber für gewöhnlich nur mit sehr großem Zeitaufwand herzustellen. Sie können nicht nur mit Zahlen, sondern sogar mit Formeln hantieren, diese umformen, einsetzen, zusammenfassen und zerlegen. Sie können Gleichungen lösen, die einfachen exakt, die komplexeren mit beliebiger Näherung. Sie können Iterationen ausführen, Grenzwerte bestimmen. Sie können ableiten und integrieren. Sie können geschwind mit Matrizen operieren, von Hand eine ermüdende, langwierige, stupide Rechenarbeit. Sie können umfangreiches Datenmaterial strukturieren. Und wo das alles noch nicht genug ist, oder wo man genauer wissen möchte, wie das alles tief im Innern vor sich geht, kann man ihre Fähigkeiten durch kleine oder größere Programme erweitern, vertiefen oder anlysieren.

Sie können uns den Kopf freihalten für wichtige Fragen: Was ist zu tun? Welcher Zusammenhang spielt eine Rolle? Wo finde ich eine Gleichung? Welche Größen können eine Rolle spielen? Welchen Zusammenhängen lohnt es nachzugehen? Welchen Einfluss haben diese oder jene Parameter? Gibt es verwandte Probleme? Sind die Ergebnisse glaubhaft? Darf man dies oder jenes voraussetzen? Wo könnte es Schwierigkeiten geben? Warum geht das eine aber das andere nicht? Sie können Denkfehler aufdecken, indem sie schnell die Konsequenzen berechnen. Sie ermöglichen, Hypothesen zu formulieren, Vermutungen zu überprüfen, Lösungsmöglichkeiten zu vergleichen, Wertungen vorzunehmen. Sie erlauben, in der Schule Mathematik auch in jenen lebensnahen Bereichen einzusetzen, die auf Grund ihrer Unhandlichkeit bislang vermieden wurden. Sie zeigen, auf wie vielfältige Weise Mathematik unseren Alltag bestimmt, bei der Verkehrssteuerung und der Computertomographie, beim Satelliten-Navigationssystem und bei der Public-Key-Verschlüsselung, bei der Heizungsregelung und der Wiedergabe von Musik-CDs.

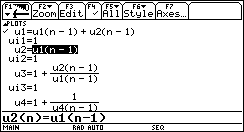
Um Missverständnissen vorzubeugen: Natürlich soll im Mathematikunterricht nun nicht der althergebrachte Stoff durch "Knöpfchen-Drücken" ersetzt werden. Natürlich soll noch gelernt werden, einfache Rechnungen oder einfache Skizzen auch ohne technische Hilfe zustande zu bringen. Natürlich sollte man wissen, nach welchem Verfahren man die vom Taschencomputer in Sekundenschnelle ausgeworfene Lösung einer Gleichung oder eines Gleichungssystems auch ohne Rechner erhalten kann. Schematisches allerdings erledigen die Maschinen schneller und sicherer, als es uns von Hand möglich ist. Da in der Arbeitswelt heute aber überall technisches Gerät zur Verfügung steht, muss nicht mehr der Umgang mit unbequemem Zahlenmaterial geübt werden. Was später von den Jugendlichen verlangt wird, ist nicht die schnelle Abwicklung von Standard-Rechenverfahren, sondern die Fähigkeit, in komplexen Situationen auf früher gewonnene Erkenntnisse zurückzugreifen, diese gedanklich richtig zu kombinieren und dann das jeweils vorhandene technische Gerät sinnvoll zu nutzen.¹

Diese Einsichten sind auch in den zukünftigen Rahmenrichtlinien Mathematik für die Klassen 7 - 10 des Gymnasiums formuliert:

„Mit elektronischen Hilfsmitteln sind differenzierte Problemstellungen und realitätsnahe Anwendungssituationen eher zugänglich. Sie erweitern die Möglichkeiten gezielten Experimentierens [. . .] Graphikfähige Taschenrechner und Computer-Algebra-Systeme [. . .] verringern die Rechenzeit und die Fehlerhäufigkeit in numerischen, kalkül-belasteten Lösungsteilen. Sie setzen Zeit frei zur Entwicklung der Problemstellung und zur Diskussion und Interpretation der Ergebnisse. Tradierte Fertigkeiten wie Kopfrechnen, Abschätzen, schriftliches Lösen sowie Skizzieren, Konstruieren, Zeichnen von Graphen und Entwerfen von Übersichten behalten dennoch Bedeutung.”

Ziel ist dabei auch, ein Gefühl für den Einsatz problemadäquater Hilfsmittel zu entwickeln. So wie wir zu Fuß gehen, wenn wir nur mal um die Ecke wollen, zum Fahrrad greifen, um fünf Straßen weiter einen Besuch zu machen, aber das Auto nehmen, wenn es sich um große Strecken oder schwere Lasten handelt, sollte man es auch beim Rechnen halten. Das Prinzip als solches bleibt selbst dann noch richtig, wenn der eine oder andere in Puschen mit dem Auto zum Zigarettenautomaten an der nächsten Ecke fährt. - Die Aufstellung ist unvollständig: irgendwo stoßen auch Taschencomputer an ihre Leistungsgrenzen, z. B. wenn es um riesige Datenmengen oder endlose Iterationen handelt. Dann ist wohl oder übel ein richtiger Computer gefragt, entsprechend dem Flugzeug für interkontinentale Entfernungen.

Zusammenfassend noch einmal die Argumente für den Einsatz von Taschencomputern im Mathematikunterricht:

• Sie können von Hand vorgenommene Rechnungen und Umformungen kontrollieren.
• Sie schulen den Blick für die Struktur der einzugebenden Formeln.
• Sie erleichtern umfangreiche Rechnungen.
• Sie entlasten von zeitraubenden und fehleranfälligen Umformungen.
• Sie veranschaulichen mathematische Zusammenhänge durch jederzeit abrufbare graphische Darstellungen.
• Sie ermöglichen zielgerichtetes Experimentieren, ...
• ... die Überprüfung zahlreicher Einzelbeispiele, ...
• ... das Bearbeiten realitätsnaher Anwendungen.
• Sie fangen punktuelle Schwierigkeiten auf, so dass die Schüler/innen trotzdem erfolgreich weiterarbeiten können.
• Sie fördern mathematisches Verständnis durch die Möglichkeit, Probleme in verschiedener Einkleidung anzugehen.
• Sie sind ständig verfügbar - im Unterricht - bei den Hausaufgaben - auch bei Klassenarbeiten, ...
• ... so dass z. B. Leistungskontrollen genau der im Unterrichtsgang eingesetzten Methode folgen.
• Sie können jederzeit - auch spontan - im Unterricht eingesetzt werden.
• Sie begleiten die Schüler/innen über Jahre und werden so allmählich vertraut und selbstverständlich.
• Sie machen gegenseitiges Aushelfen möglich.
• Dass alle dasselbe Gerät benutzen, ist ein Beitrag zur Chancengleichheit.
• Und schließlich ist auch ein Ausleihsystem für Härtefälle finanzierbar.

Aber natürlich ist selbst mit diesem Gerät der Nürnberger Trichter nicht erfunden. Als vor über zweitausend Jahre Euklid die Geometrie seiner Zeit in den „Elementen” streng logisch zusammengefasst hatte, fragte ihn König Ptolemäus Philadelphos, ob es für die Aneignung der Mathematik keinen bequemeren Weg gebe. Die Antwort „Für die Mathematik gibt es keinen Königsweg” gilt im 21. Jahrhundert immer noch. Sie gelangt trotz eines so vielseitigen Werkzeugs nicht mühelos und anstrengungsfrei in die Köpfe. Vielmehr sind weiterhin Konzentration und Mitdenken, Arbeitsbereitschaft und Sachinteresse, Offenheit und Problembewusstsein vonnöten, um im Mathematikunterricht erfolgreich mithalten und mitgestalten zu können. Der Arbeitsschwerpunkt hat sich verschoben, aber die Arbeit ist geblieben. Und es ist immer noch dabei geblieben, dass auch mit den tollsten Hilfsmitteln nicht jeder alles erreichen kann. Dass mag uns alle, Lehrer, Eltern und Schüler, mit Bescheidenheit erfüllen und vor falschen Hoffnungen bewahren.